Soft Thresholding

Definition

Given a function \(f : \RR^n \to (-\infty, \infty]\), the proximal mapping of \(f\) is the operator given by

\[\text{prox}_f(x) = \text{argmin}_u \left \{ f(u) + \frac{1}{2} \| u - x \|_2^2 \right\} \quad \forall x \in \RR^n.\]

The proximal mapping in general is a point to set mapping. i.e. it maps each point \(x \in \RR^n\) to a set of points in \(\RR^n\) which minimize the expression on the R.H.S.

When \(f\) is a proper closed convex function, then the set \(\text{prox}_f(x)\) is a singleton for each \(x \in \RR^n\). In this case, proximal mapping can be treated as a single valued mapping or a function.

Proposition

Let \(f(x) = c\), then \(\text{prox}_f(x) = x\).

Proof

Let

\[g_x(u) = f(u) + \frac{1}{2} \| u - x \|_2^2 = c + \frac{1}{2} \| u - x \|_2^2.\]

To minimize \(g\) over \(u\), we differentiate \(g\) w.r.t. \(u\).

\[\frac{\partial g}{\partial u} = u - x.\]

The minimum value is achieved at \(u = x\).

A simpler argument is that \(g\) is a constant plus a quadratic. Thus, the minimum of \(g\) is achieved when the quadratic is 0 which happens when \(x = u\).

Proposition

Let \(f : \RR \to \RR\) be defined as \(f(x) = x\), then \(\text{prox}_f(x) = x - 1\).

Proof

Let

\[g_x(u) = f(u) + \frac{1}{2} (u - x)^2 = u + \frac{1}{2} (u - x)^2.\]

To minimize \(g\) over \(u\), we differentiate \(g\) w.r.t. \(u\).

\[\frac{\partial g}{\partial u} = 1 + u - x.\]

The minimum value is achieved at \(u = x - 1\).

Proposition

Let \(f : \RR \to \RR\) be defined as \(f(x) = \lambda x\), then \(\text{prox}_f(x) = x - \lambda\).

Proposition

Let \(f\) be defined as:

\[\begin{split}f(x) = \begin{cases} \lambda x & \text{if $x \geq 0$}\\ \infty & \text{otherwise} \end{cases}\end{split}\]

Then \(\text{prox}_f(x)\) is \([x - \lambda]_+\).

This is one-sided soft-thresholding.

Proof

Note that \(f\) is differentiable for \(x > 0\). \(\text{prox}_f(x)\) is the minimizer of the function

\[\begin{split}g(u) = \begin{cases} g_1(u) & u \geq 0 \\ \infty & u < 0 \end{cases}\end{split}\]

where

\[g_1(u) = \lambda u + \frac{1}{2} (u - x)^2.\]

\(g\) is a proper, convex and closed function. \(g\) is differentiable for \(u > 0\) with \(g'(u) = g_1'(u)\) for \(u > 0\). The only point where \(g\) is non-differentiable is \(u = 0\) in the domain of \(g\) which is \(u \geq 0\).

If \(g'(u) = 0\), then \(u\) is a minimizer of \(g\) (since it is a convex function).

\(g_1'(u) = 0\) iff \(u = x - \lambda\). If \(x > \lambda\), then \(g'(x-\lambda) = g_1'(x-\lambda) = 0\). Thus, \(\text{prox}_f(x) = x - \lambda\) for \(x > \lambda\).

Now if \(x \leq \lambda\), the \(g'(u)\) is never 0 wherever \(g\) is differentiable. Since a minimum of \(g\) exists, it must be attained at a point of non-differentiability. The only point of non-differentiability is \(u = 0\). Thus, \(\text{prox}_f(x) = 0\) for \(x \leq \lambda\).

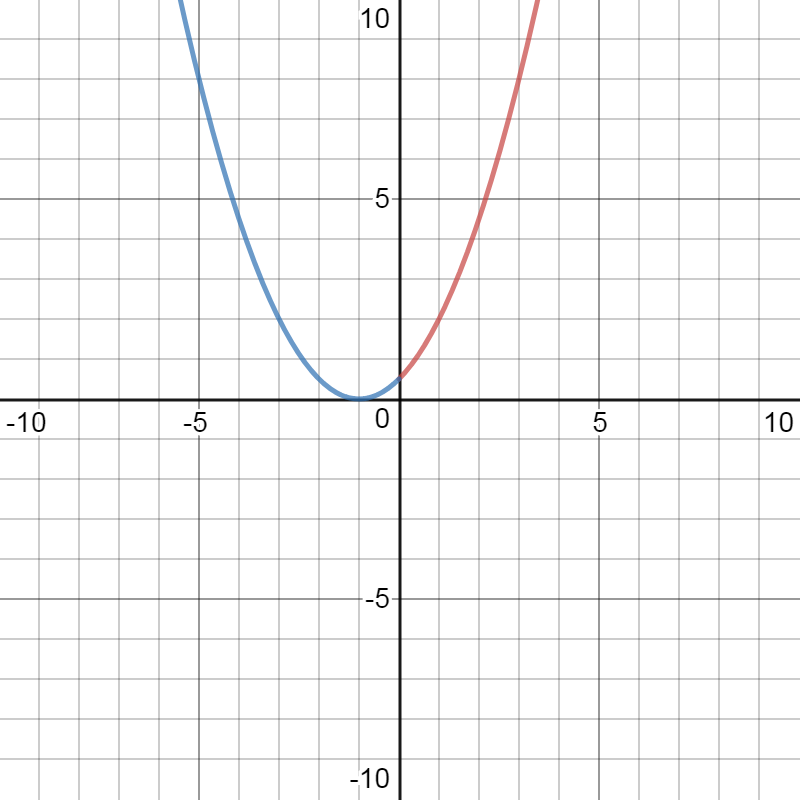
The quadratic \(g(u) = 2u + \frac{1}{2} (u - 1)^2\). If the \(2u\) term was not present, the minimum would have been \(u = 1\). The term \(2u\) just shifts the minimum left by 2 to \(u = -1\). However, if the domain of the function is restricted to \(u \geq 0\) (the red part of the graph), then the minimum is achieved at \(u = 0\).

For general \(g(u) = \lambda u + \frac{1}{2}(u - x)\) with domain limited to \(u \geq 0\), as long as \(x \geq \lambda\), the minimum is achieved at \(u = x - \lambda\). For all \(x < \lambda\), the minimum is achieved at \(u = 0\).

Proposition

Let \(f : \RR \to \RR\) be defined as \(f(x) = \lambda |x|\), then

\[\text{prox}_f(x) = [|x| - \lambda]_+ \sgn(x).\]

Proof

Note that \(f\) is differentiable for \(x \neq 0\). \(\text{prox}_f(x)\) is the minimizer of the function

\[\begin{split}g(u) = \begin{cases} g_1(u) = \lambda u + \frac{1}{2} (u - x)^2 & u \geq 0 \\ g_2(u) = -\lambda u + \frac{1}{2} (u - x)^2 & u < 0 \end{cases}\end{split}\]

If a minimizer is obtained at \(u > 0\), then \(0 = f'(u) = g_1'(u) = \lambda + u - x\) giving us \(u = x - \lambda\). Since, we assumed that \(u > 0\), hence \(x > \lambda\). In other words, if \(x > \lambda\), then \(u = x - \lambda\) is the minimizer. Similarly, for \(x < -\lambda\), \(u = x + \lambda\) is the minimizer. For \(-\lambda \leq x \leq \lambda\), the minimizer is at the only point of non-differentiability for \(g_1\) which is \(u = 0\). Thus

\[\begin{split}\text{prox}_f(x) = \begin{cases} x - \lambda & x > \lambda \\ 0 & -\lambda \leq x \leq \lambda \\ x + \lambda & x < -\lambda \end{cases}\end{split}\]

This is nothing but shrinkage operator or soft thresholding operator.

Definition

The soft thresholding operator \(S: \RR \to \RR\) is defined as:

\[\begin{split}S_{\kappa}(x) = \begin{cases} x - \kappa & x > \kappa \\ 0 & |x| \leq \kappa \\ x + \kappa & x < -\kappa \end{cases}.\end{split}\]

An equivalent definition is

\[S_{\kappa}(x) = (x - \kappa)_+ - (-x-\kappa)_+.\]

Proposition

The minimizer of

\[f(x) = \lambda |x| + \frac{1}{2} (x - u)^2\]

is \(S_{\lambda}(u)\).

This is a straight-forward application of the proximal operator result above.

Proposition

The minimizer of

\[f(x) = \lambda |x| + \frac{\rho}{2} (x - u)^2\]

is \(S_{\lambda/\rho}(u)\).

Proof

\[\begin{split}f(x) = \begin{cases} f_1(x) = \lambda x + \frac{\rho}{2} (x - u)^2 & x \geq 0 \\ f_2(x) = -\lambda x + \frac{\rho}{2} (x - u)^2 & x < 0 \end{cases}.\end{split}\]

\(f\) is differentiable everywhere except at \(x = 0\).

If a minimizer is obtained at \(x > 0\), then

\[0 = f'(x) = f_1'(x) = \lambda + \rho (x - u)\]

giving us \(x = u - \frac{\lambda}{\rho}\). This holds true if \(u > \frac{\lambda}{\rho}\). Rest of the argument is similar.

Definition

Element-wise soft thresholding operator \(S_{\lambda} : \RR^n \to \RR^n\) is defined as

\[\begin{split}S_{\lambda}(x_i) = \begin{cases} x_i - \lambda & x_i > \lambda \\ 0 & |x_i| \leq \lambda \\ x_i + \lambda & x_i < -\lambda \end{cases}.\end{split}\]

Proposition

The minimizer of \(f: \RR^n \to \RR\) defined as

\[f(x) = \lambda \|x\|_1 + \frac{\rho}{2} \|x - u\|_2^2\]

is \(S_{\lambda/\rho}(u)\) (applied element-wise).

Proof

The result follows from the fact that \(f(x)\) is separable as \(f(x) = \sum f_i(x_i)\) where

\[f_i(x) = \lambda |x_i| + \frac{\rho}{2} (x_i - u_i)^2.\]

Definition

Element-wise soft thresholding operator over matrices \(S_{\lambda} : \RR^{m\times n} \to \RR^{m\times n}\) is defined as

\[\begin{split}S_{\lambda}(x_{ij}) = \begin{cases} x_{ij} - \lambda & x_{ij} > \lambda \\ 0 & |x_{ij}| \leq \lambda \\ x_{ij} + \lambda & x_{ij} < -\lambda \end{cases}.\end{split}\]

Proposition

The minimizer of \(f: \RR^{m \times n} \to \RR\) defined as

\[f(X) = \lambda \|X\|_{1,1} + \frac{\rho}{2} \|X - U\|_F^2\]

is \(S_{\lambda/\rho}(U)\) (applied element-wise).

See Row column norms for formal definition of \(\| \cdot \|_{1,1}\) norm. It is essentially the absolute sum of all elements of a matrix.

Proof

The result follows from the fact that \(f(x)\) is separable over all elements of \(X\).